numpy.polynomial.laguerre.lagvander3d
-
numpy.polynomial.laguerre.lagvander3d(x, y, z, deg)[source] -
Pseudo-Vandermonde matrix of given degrees.
Returns the pseudo-Vandermonde matrix of degrees
degand sample points(x, y, z). Ifl, m, nare the given degrees inx, y, z, then The pseudo-Vandermonde matrix is defined by![V[..., (m+1)(n+1)i + (n+1)j + k] = L_i(x)*L_j(y)*L_k(z),](https://docs.scipy.org/doc/numpy-1.12.0/_images/math/6743bc74d241f8b198daf8f5bb91a4f3f1fbabca.png)
where
0 <= i <= l,0 <= j <= m, and0 <= j <= n. The leading indices ofVindex the points(x, y, z)and the last index encodes the degrees of the Laguerre polynomials.If
V = lagvander3d(x, y, z, [xdeg, ydeg, zdeg]), then the columns ofVcorrespond to the elements of a 3-D coefficient arraycof shape (xdeg + 1, ydeg + 1, zdeg + 1) in the order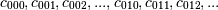
and
np.dot(V, c.flat)andlagval3d(x, y, z, c)will be the same up to roundoff. This equivalence is useful both for least squares fitting and for the evaluation of a large number of 3-D Laguerre series of the same degrees and sample points.Parameters: x, y, z : array_like
Arrays of point coordinates, all of the same shape. The dtypes will be converted to either float64 or complex128 depending on whether any of the elements are complex. Scalars are converted to 1-D arrays.
deg : list of ints
List of maximum degrees of the form [x_deg, y_deg, z_deg].
Returns: vander3d : ndarray
The shape of the returned matrix is
x.shape + (order,), where![order = (deg[0]+1)*(deg([1]+1)*(deg[2]+1)](https://docs.scipy.org/doc/numpy-1.12.0/_images/math/d7ba451e95493b79a58a12206ce9ce68c2d3d7a5.png) . The dtype will be the same as the converted
. The dtype will be the same as the converted x,y, andz.Notes
© 2008–2017 NumPy Developers
Licensed under the NumPy License.
https://docs.scipy.org/doc/numpy-1.12.0/reference/generated/numpy.polynomial.laguerre.lagvander3d.html