numpy.polynomial.chebyshev.chebgrid2d

numpy.polynomial.chebyshev.chebgrid2d(x, y, c) [source]

Evaluate a 2-D Chebyshev series on the Cartesian product of x and y.

This function returns the values:

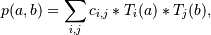
where the points (a, b) consist of all pairs formed by taking a from x and b from y. The resulting points form a grid with x in the first dimension and y in the second.

The parameters x and y are converted to arrays only if they are tuples or a lists, otherwise they are treated as a scalars. In either case, either x and y or their elements must support multiplication and addition both with themselves and with the elements of c.

If c has fewer than two dimensions, ones are implicitly appended to its shape to make it 2-D. The shape of the result will be c.shape[2:] + x.shape + y.shape.

Parameters:

x, y : array_like, compatible objects The two dimensional series is evaluated at the points in the Cartesian product of x and y. If x or y is a list or tuple, it is first converted to an ndarray, otherwise it is left unchanged and, if it isn’t an ndarray, it is treated as a scalar. c : array_like Array of coefficients ordered so that the coefficient of the term of multi-degree i,j is contained in c[i,j]. If c has dimension greater than two the remaining indices enumerate multiple sets of coefficients.

Returns:

values : ndarray, compatible object The values of the two dimensional Chebyshev series at points in the Cartesian product of x and y.

See also

chebval, chebval2d, chebval3d, chebgrid3d

Notes